浮点数计算时有个很常见的精度case是0.1+0.2!=0.3,网络上有很多文章剖析了为啥0.1+0.2!=0.3,然后给出了解决方案:将各个浮点数乘以一个高倍数再进行计算,或者判断差值小于一个值,就可以了。
确实,0.1*1000+0.2*1000==0.3*1000。但是能否就这样处理浮点数比较的问题呢?
实际上网上很多文章都是错误的,所以即使有意识的去规避,还是踩到了这样的一个坑:16.1*1000!=16100。之后才发现以前都是只知道有这个现象,也有意识规避它,但是实际上并没有深入去理解原理,对网上的策略也没做深入思考,所以规避的并不彻底,所以有此文章做一下总结。
1.浮点数的二进制存储方法
1.1 存储原理
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。引自IEEE 754 wikipedia。
由于我遇到这个问题是在js中,而js的number类型统一用64位浮点数来表示,所以本文只研究64位的情况,32位的浮点数原理上是相同的。
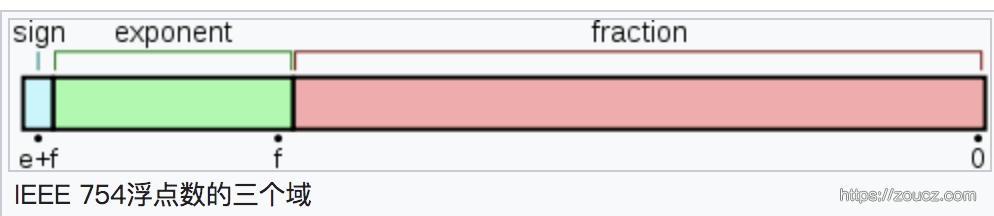
最高为的1位为S,符号位;后面跟着的11位为指数位 E;后面52位为有效数字位 M。
那么任意一个浮点数V可以表示为: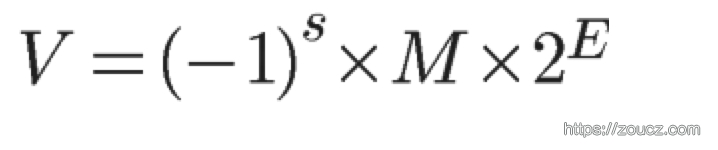
其中
- 符号位s为0时,浮点数是正数,为1时浮点数是负数
- M是52位的有效数字,这也是为啥js中数字的最大精度在
2^53-1的原因 - E是11位的指数
在实际存储的时候,有效数字M部分,由于M表示有效数字,值总是在1~2之间,所以存储时可以省掉最前面的1,读取时再给拼上,这样就能节省1位的存储空间;
指数E部分,为了方便的比较大小,实际存储时用的是一个unsigned int的方式,但是指数实际使用的时候是会有负数的情况的,所以指数存储的时候会加1023后存储为unsigned int,读取的时候也会先读出来再减去1023,所以E的范围是1~2046,0和2047表示特殊值,详见wiki。
1.2 实验
写一段nodejs的代码用来分析浮点数在二进制中的表示,把文首的几位主角拿出来跑一跑:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21function float2binstr(f:number) {
let buf = Buffer.allocUnsafe(8)
buf.writeDoubleBE(f)
let binstr = ""
for(let i=0;i<8;i++){
binstr+=buf[i].toString(2).padStart(8, "0")
}
let formatBinstr = `符号:${binstr[0]} 指数:${binstr.slice(1, 12)} 有效数字:${binstr.slice(12)}`
console.log("浮点数:", f)
console.log("二进制:", formatBinstr)
console.log("科学计数法:", `(-1)^${binstr[0]}*1.${binstr.slice(12)}*2^${Number(`0b${binstr.slice(1, 12)}`)-1023}`)
}
float2binstr(0.1)
float2binstr(0.2)
float2binstr(0.3)
float2binstr(0.1+0.2)
float2binstr(16.1)
float2binstr(1000)
float2binstr(16100)
float2binstr(16.1*1000)
输出结果:
很容易发现,造成进度问题的根本原因是,在运算之后,有效数字位M的最低几位与未丢失精度时的值相比,发生了变化。
2.二进制四则运算与精度丢失的原因
2.1 二进制四则运算规则
上面可以发现是运算的过程中使有效数字末尾的精度发生了变化,这里看看为什么会造成这种变化。
首先是运算规则,加减法:
1 | 1)对阶,使得两数的小数点位置对齐。 |
乘除法:
1 | 1)阶码相加减:按照定点整数的加减法运算方法对两个浮点数的阶码进行加减运算。 |
2.2 case分析
本文两个例子中,0.1+0.2的过程:
①对阶:将科学计数法中的指数位应用到有效数字上改变小数点位置,让小数点对齐
1 | 0.1:0.00011001100110011001100110011001100110011001100110011010 |
②求和:随便找个在线二进制加法计算器算一把
1 | 0.00011001100110011001100110011001100110011001100110011010 + |
③规格化:为了增加有效位数,将执行一个反对阶操作
1 | 0.01001100110011001100110011001100110011001100110011010000 = |
④存储&舍入:存储时只有52位可用,对丢弃的部分做舍入判断,ieee754有4种策略,这里使用默认策略
1 | 有效位:1.001100110011001100110011001100110011001100110011010000 |
⑤溢出判断
未溢出
与0.3的有效位对比:
1 | 0011001100110011001100110011001100110011001100110100 —— 0.1+0.2 |
比较好发现,精度末尾的地方多出来了4。
16.1*1000的过程:
①阶码相加
1 | 9 + 4 + 1023 = 10000001100 |
②尾数相乘
1 | 1.0000000110011001100110011001100110011001100110011010 * |
③规格化与舍入:根据结果位数可知并没有发生进位
1 | 存储时丢弃开头的1: |
④溢出判断
未溢出
与16100的有效位对比:
1 | 1111011100100000000000000000000000000000000000000001 —— 16.1*1000 |
这也是为啥 16.1*1000!=16100 ,且最后面多了个1。
2.3 规律总结
总之,由于js的数字都有float64表示,且十进制与二进制进位数字的不同,精度问题不能从直觉上用网上很多文章所说的小数变整数再计算来回避,因为js没有“整数”。
正如十进制在 有限的表示空间内, 同样无法用小数准确表示1/3、3/7这类无限循环小数一样,二进制下基本上所有涉及到“分数”的计算都有此隐患,参与计算的数字会因为存储空间的原因丢失一部分精度,或小一点点,或大一点点。类似的例子还有 0.14*10!=1.4、0.3*3!=0.9 等等。
那么哪些case无此隐患呢?
1 | float2binstr(1*Math.pow(2, -1)) |
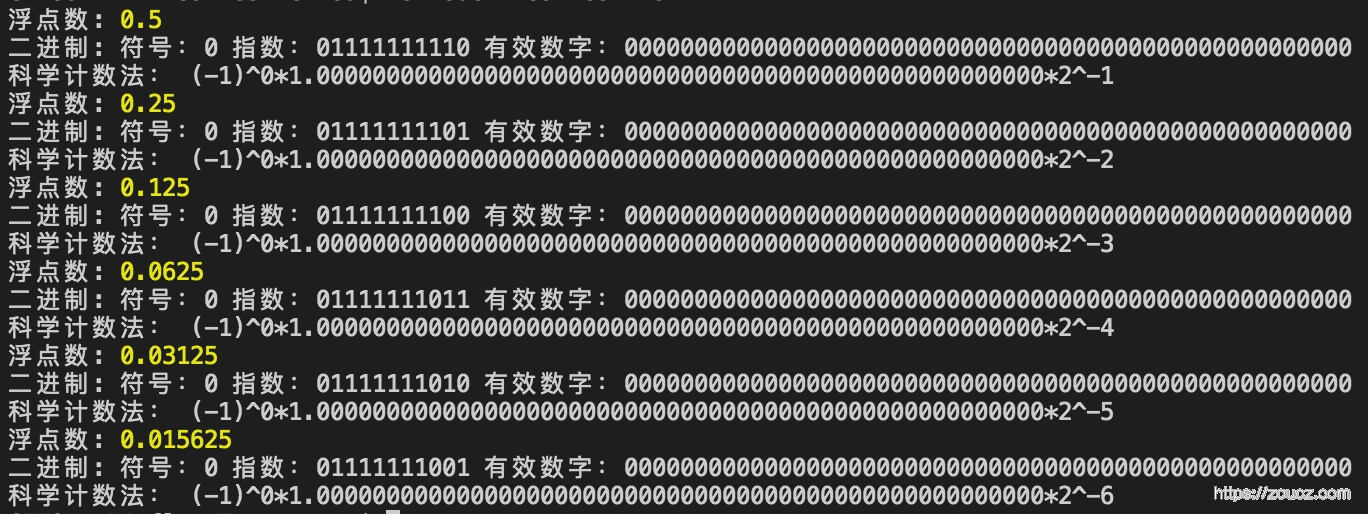
这些规整的有效数字,都是不会有隐患的。
3.哪些语言有这种现象
- js:所有数字都用float64表示,基本所有涉及小数的计算都有此问题
- python:python的浮点数据类型使用底层表示存储数据,在ieee 754标准下,存在此问题
- java:java的浮点数完全遵循eee 754标准,存在此问题
- go:go的浮点数完全遵循eee 754标准,存在此问题
- c++:c++的浮点数完全遵循eee 754标准,存在此问题
- …
但凡没有自己实现基于十进制的数字运算的语言,都有此问题!
这里有一点值得注意的是,js所有数字都是float64,但很多语言都支持单精度、双精度浮点数的。
例如用c++写:1
2
3
4float a = 0.1;
float b = 0.2;
float c = 0.3;
std::cout << "0.1+0.2==0.3:" << (a+b==c) << std::endl;
这个判等的结果是true,然而将单精度的float换成双精度的double,判等的结果就是false了。
这里的原因是不同的存储空间,丢弃数据时的位置不同,所以单双精度浮点数产生精度问题的点位可能就不通。这并不代表单精度浮点数就不会有精度问题了!
可以写个demo把二进制输出看一下,如果使用单精度浮点数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17function float2binstr(f:number) {
let buf = Buffer.allocUnsafe(4)
buf.writeFloatBE(f)
let binstr = ""
for(let i=0;i<4;i++){
binstr+=buf[i].toString(2).padStart(8, "0")
}
let formatBinstr = `符号:${binstr[0]} 指数:${binstr.slice(1, 9)} 有效数字:${binstr.slice(9)}`
console.log("浮点数:", f)
console.log("二进制:", formatBinstr)
console.log("科学计数法:", `(-1)^${binstr[0]}*1.${binstr.slice(9)}*2^${Number(`0b${binstr.slice(1, 9)}`)-127}`)
}
float2binstr(0.1)
float2binstr(0.2)
float2binstr(0.3)
float2binstr(0.1+0.2)
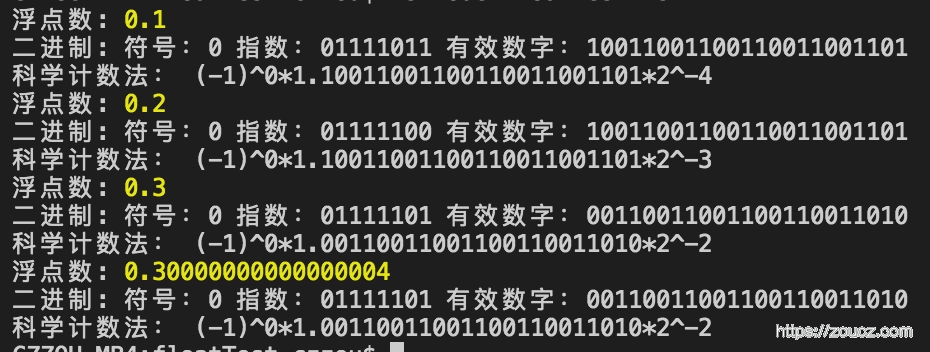
可以看到有效数字是一样的。如果js支持单精度浮点数的话,0.1+0.2==0.3的结果也会是true。
4.精确运算与比较的实现
上面提出了问题,那么如何解决问题呢?
4.1 比较
网上说的乘以高倍数不可行,但是判断差值小于某个值还是可行的。
例如可以使用 Number.EPSILON 常量1
2
3
4x = 0.2;
y = 0.3;
z = 0.1;
equal = (Math.abs(x - y + z) < Number.EPSILON);
这样做比较就可以了。
4.2 计算
比较是没问题了,但是要实现十进制意义上的精确浮点数运算,可以用一些库来实现,例如 decimal.js 库。1
2
3
4
5import Decimal from "decimal.js"
let a = new Decimal(0.1)
let b = a.add(0.2)
console.log(b.toNumber())
//输出十进制意义上的精确结果:0.3
看库的名字就知道,这是一个实现十进制运算的库,规避掉了二进制小数运算时产生的精度丢弃,与十进制运算直觉不一致的问题。
当然它的性能会比系统底层的浮点数运算低的多的多,在考虑符合直觉而不考虑性能的地方,可以考虑使用。
一个简单的benchmark:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20import Decimal from "decimal.js"
let start = new Date()
for(let i=0;i<1000000;i++){
let a = new Decimal(0.1)
let b = a.add(0.2)
}
let end = new Date()
console.log("decimal cost:", end.getTime() - start.getTime())
start = new Date()
for(let i=0;i<1000000;i++){
let a = 0.1
let b = 0.2
let c = a+b
}
end = new Date()
console.log("native cost:", end.getTime() - start.getTime())
//decimal cost: 1234
//native cost: 2
本文链接:https://www.zoucz.com/blog/2021/07/08/52c9e5d0-dfb5-11eb-9fe7-534bbf9f369d/
